문제 링크: https://www.acmicpc.net/problem/2344
2344번: 거울
세로 N, 가로 M 크기의 상자가 있다. 이 상자 안에는 몇 개의 거울이 들어 있다. 상자를 위에서 봤을 때, 거울은 한 칸 안에 대각선 모양으로 들어있다고 한다. 또, 상자의 테두리를 따라서 칸마다
www.acmicpc.net
문제 풀이
시뮬레이션
전형적인 시뮬레이션 문제이다.
5 4
0 1 0 0
0 0 1 0
0 0 1 0
0 0 0 1
0 1 0 0 으로 주어졌을 때를 시뮬레이션 해보자.
1~5번의 경우는 다음과 같다.
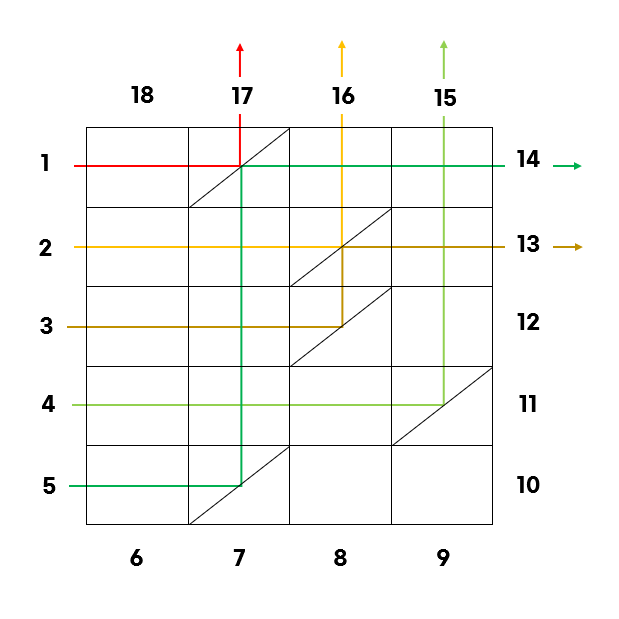
좌표와 방향을 이용해서 적절하게 풀 수 있다. 이때 x는 0보다 크거나 같고 n보다 작고 y는 0보다 크거나 같고 m보다 작으면 반복문을 종료시킨다. 방향은 1~5번일 때 →로 시작하게 된다. 이때의 방향을 0이라고 하자.
0일때는 y가 1씩 증가한다.
마찬가지로, ↓는 1로 하면 x가 1씩 증가하고,
←는 2로 하면 y가 1 감소하고,
↑는 3으로 하면 x가 1씩 감소한다.
1번의 좌표는 (0, 0)에서 시작하고 (0, 1)에서 거울을 만나므로 방향을 3으로 바꿔주고 다시 이동한다. 그러면 (-1, 1)로 가질테니 반복문을 종료시키자.
2번의 좌표는 (1, 0)에서 시작하고 (0, 2)까지 가다가 거울을 만나 방향이 3으로 바뀌고 (0, 2)로 이동하다가 (-1, 2)로 가서 종료된다.
3번의 좌표는 (2, 0)에서 시작하고 (2, 2)에서 방향이 3으로 변경되고 (1, 2)에서 다시 거울을 만나 (1, 4)으로 가므로 종료한다.
이런 식으로 x, y좌표를 이용해서 나가는 곳을 알아보면 다음과 같다.
1. 1~5번으로 빠져나가는 경우는 y가 음수가 될 때이다.
: 1~5번의 경우는 x+1번이 된다. 예를 들어 x, y좌표가 (2, -1)에서 종료될 경우 2+1번, 즉 3번이 된다.
2. 6~9번으로 빠져나가는 경우는 x가 n과 같을 때이다.
: 이 경우는 n+y+1번이 된다. 예를 들어 x, y좌표가 (5, 2)에서 종료될 경우는 5+2+1번, 즉 8번이 된다.
3. 10~14번으로 빠져나가는 경우는 y가 m과 같을 때이다.
: 이 경우는 n+m+(n-x)번이 된다. 예를 들어, x, y좌표가 (2, 4)에서 종료될 경우 5+4+(5-2)번, 즉 12번이 된다.
4. 15~18번으로 빠져나가는 경우는 x가 음수가 될 때이다.
: 이 경우는 2*n+m+(m-y)이 된다. 예를 들어, x, y좌표가 (-1, 1)에서 종료될 경우 2*5+4+(4-1)번, 즉 17번이 된다.
이런 식으로 시뮬레이션을 돌려서 1번 입구부터 18번 입구까지의 경우를 모두 구한다. 자그만한 꿀팁이라면 방향은 0, 3으로 서로 바뀌고 1, 2로 서로 바뀐다.
코드
'BOJ' 카테고리의 다른 글
| [BOJ][Python] 백준 4696번 - St. Ives (0) | 2022.08.02 |
|---|---|
| [BOJ][Python] 백준 11434번 - Ampelmännchen (0) | 2022.08.02 |
| [BOJ][Python] 백준 20412번 - 추첨상 사수 대작전! (Hard) (0) | 2022.07.02 |
| [BOJ][Python] 백준 10172번 - 개 (0) | 2022.05.05 |
| [BOJ][C] 백준 10430번 - 나머지 (0) | 2022.05.05 |